Intro
Warping, or dommain distortion is a very common technique in computer graphics for generating procedural textures and geometry. It's often used to pinch an object, strech it, twist it, bend it, make it thicker or apply any deformation you want. It works as long as your base color pattern or geometry is defined as a function of space. In this article I'm only going to show a very particular case of warping - noise based warping or a noise function. This has been used since 1984, when Ken Perlin himself created his first procedural marble texture.

The basics
Say you have some geometry or image defined as a function of space. For geometry, that would be a function of the form f(x,y,z) and for an image it would be f(x,y). We can just write both cases more compactly as f(p), where p is the position in space for which we can evaluate the volumetric density that will define our (iso)surface or image color. Warping simply means we distort the domain with another function g(p) before we evaluate f. Basically, we replace f(p) with f(g(p)). g can be anything, but often we want to distort the image of f just a little bit with respect its regular behaviour. Then, it makes sense to have g(p) being just the identity plus a small arbitrary distortion h(p), or in other words,
g(p) = p + h(p)
meaning we will be computing
f( p + h(p) )
This technique is really powerfull and allows you to shape apples, buildings, animals or any other thing you might imagine. For the purpose of this article, we are going to work only with fBM based patterns, both for f and h. This will produce some abstract but beautiful images with a pretty organic quality to them.
The idea
So we are going to use some standard fBM (Fractional Brownian Motion) which is a simple sum of noise waves with increasing frequencies and decreasing amplitudes).
A simple fBM is displayed in the first image to the right. The code looks like this:
float pattern( in vec2 p )
{
return fbm( p );
}
We can now add a first domain warping (second image to the right):
float pattern( in vec2 p )
{
vec2 q = vec2( fbm( p + vec2(0.0,0.0) ),
fbm( p + vec2(5.2,1.3) ) );
return fbm( p + 4.0*q );
}
Note how we use two 1-dimensional fBM calls to emulate a 2-dimensional fBM, which is what we need in order to displace a point in 2 dimensions.
Lastly, we add the second wraping (third image to the right):
float pattern( in vec2 p )
{
vec2 q = vec2( fbm( p + vec2(0.0,0.0) ),
fbm( p + vec2(5.2,1.3) ) );
vec2 r = vec2( fbm( p + 4.0*q + vec2(1.7,9.2) ),
fbm( p + 4.0*q + vec2(8.3,2.8) ) );
return fbm( p + 4.0*r );
}
Of course those particular offset values in the 2-dimensional fBM emulation through 1-dimensional fbm() calls don't have any special meaning, they are used to get different fBM values by using one single fbm() implementaiton.

Image for f(p) = fbm( p )
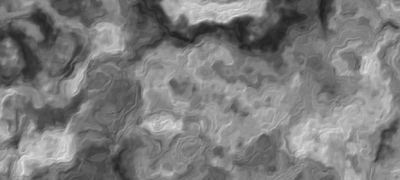
Image for f(p) = fbm( p + fbm( p ) )

Image for f(p) = fbm( p + fbm( p + fbm( p )) )
The experiments
Now the basics are set, it's time to start playing around. First obvious idea is to introduce time as a parameter to get some sort of animation. That you can probably figure out by yourself. Results are pretty cool. Look in the following video (sorry for the low quality enconding, I made it in 2002), or to the last video in the bottom of this article.
Animated fbm(fbm(p)) - made in 2002
Next step is adding some colors to our images. We can simply map a color palette to our density values. That's a good start, but it's not enough. We might want to use the internal values of the funcion to get some extra color patterns and shapes. After all, we got three fBM functions that do change the internal structure of our final image, so why not use those too to get some extra coloring. The first we have to do, then, is to actually expose those values to the outside world:
float pattern( in vec2 p, out vec2 q, out vec2 r )
{
q.x = fbm( p + vec2(0.0,0.0) );
q.y = fbm( p + vec2(5.2,1.3) );
r.x = fbm( p + 4.0*q + vec2(1.7,9.2) );
r.y = fbm( p + 4.0*q + vec2(8.3,2.8) );
return fbm( p + 4.0*r );
}
Now we can start playing arround and getting some colors. For example, one could start from a simple color ramp based on f, then mix the color to a third one based on the magnitude of q and finally mix to a forth one based on the vertical component of r. Of course that is just one of the infinite amount of posibilities that we get here. In any case, doing so results in some nice colored image, like the one below or the one opening this article.

This is a video using the same idea. You can find the source code for it and the realtime animated version here: https://www.shadertoy.com/view/4s23zzM:
Using q and r to add coloring - made in 2012
And here's another one, embeded directly from https://www.shadertoy.com/view/lsl3RH (where you can find the ource code):








