You probably remember this identity from school:
sin(α+β)=sin α ⋅ cos β + cos α ⋅ sin β
cos(α+β)=cos α ⋅ cos β - sin α ⋅ sin β
When you are a kid and are first introduced to it your first feeling is the pain of having to memorize it. That's too bad, because in fact you don't need to memorize anything as this formula arises naturally when you draw the rotation of a triangle, on a piece of paper. That's actually what I do when I need this formula down but can't remember it. I draw it. You probably will be able to do so too by the time we are half way down this tutorial. But for now, and to keep the things fun and delay the eureka moment for a bit, let's first think when would we need this formula in the first place.
sin(α+β)=sin α ⋅ cos β + cos α ⋅ sin β
cos(α+β)=cos α ⋅ cos β - sin α ⋅ sin β
When you are a kid and are first introduced to it your first feeling is the pain of having to memorize it. That's too bad, because in fact you don't need to memorize anything as this formula arises naturally when you draw the rotation of a triangle, on a piece of paper. That's actually what I do when I need this formula down but can't remember it. I draw it. You probably will be able to do so too by the time we are half way down this tutorial. But for now, and to keep the things fun and delay the eureka moment for a bit, let's first think when would we need this formula in the first place.

Intro
The sin and cos trigonometric functions are probably the functions that most frequently appear in computer graphics, for they are the simplest (but not only) way to describe any circular motion and shape in a parametric way. Among their uses, we have the generation of circles or 3D revolution objects, the computation of Fourier Transforms, the synthesis of procedural waves, the creation of noise, the production of software sound synthesizer, etc etc. In all these cases, sin, cos or both are repeatedly called inside a loop, similar to this:
for( int n=0; n<num; n++ )
{
const float t = 2.0f*PI*(float)n/(float)num;
const float s = sinf(t);
const float c = cosf(t);
// do something with s and c
...
}
So let me rewrite this loop in an incremental fashion now, so that it's easier to see that given an iteration n of the loop which corresponds to a phase t, the next iteration n+1 is going to compute the sin and cos of t+f. In other words, after computing sin(t) and cos(t), the next iteration needs to compute sin(t+f) and cos(t+f):
const float f = 2.0f*PI/(float)num;
const float t = 0.0f;
for( int n=0; n < num; n++ )
{
const float s = sinf(t);
const float c = cosf(t);
// do something with s and c
...
t += f;
}
So we can try to think if there's a way to compute sin(t+f) and cos(t+f) from sin(t) and cos(t), because if there is one and it doesn't involve expensive functions like square roots or trigonometrics, then we'd be able to take the expensive evaluations of sin(t) and cos(t) out of the loop!
Well, let's look no further than the formula at the top of the article, the one we memorized as kids. According to it:
sin(t+f) = sin(f)⋅cos(t) + cos(f)⋅sin(t)
cos(t+f) = cos(f)⋅cos(t) - sin(f)⋅sin(t)
or in more coder-friendly manner:
new_sin = sin(f)⋅old_cos + cos(f)⋅old_sin
new_cos = cos(f)⋅old_cos - sin(f)⋅old_sin
Now, because f is a constant, so are cos(f) and sin(f). Let's call them a and b so that:
new_sin = b⋅old_cos + a⋅old_sin
new_cos = a⋅old_cos - b⋅old_sin
This expression can be directly used in our code, resulting in a loop that hasn't any expensive trigonometric function at all, just like we hoped for. See:
const float f = 2.0f*PI/(float)num;
const float a = cosf(f);
const float b = sinf(f);
float s = 0.0f;
float c = 1.0f;
for( int n=0; n<num; n++ )
{
// do something with s and c
...
const float ns = b*c + a*s;
const float nc = a*c - b*s;
c = nc;
s = ns;
}
The interpretation
So far we have blindly used the math identity we learnt at school without really talking about what we've been actually doing. So let's first rewrite the inner loop this way:
sn+1 = sn ⋅ a + cn⋅b
cn+1 = cn ⋅ a - sn⋅b
Some of you might have already noticed that this is nothing but the traditional way to compute 2D rotations. If you didn't recognize it, perhaps rewriting it in matrix form helps:

Indeed, sin(t) and cos(t) can be grouped as a vector of length one; let's call it x:
x = ( sin t, cos t)T
Then, the vectorial form of the expression above looks like
xn+1 = R ⋅ xn
with R being the {a, b, -b, a} 2x2 matrix. So, we see that our loop is performing a little 2D rotation in each iteration, such that x rotates in a circle during the execution of the loop. Every iteration x rotates by an angle of 2π/num radians.
So, basically
sin(α+β)=sin α ⋅ cos β + cos α ⋅ sin β
cos(α+β)=cos α ⋅ cos β - sin α ⋅ sin β
as we learnt at school, must be a 2D rotation formula of a point x = (cos(α), sin(α))T in the circle by an angle of β radians. To check that, we first construct one of the two axes of the rotation, ie, u = ( cos(β), sin(β) )T. The first component of the rotation is going to be the projection of x into u. Because both x and u have a length of one, so the projection is just their dot product. Therefore:
s = <x,u> = sin α ⋅ cos β + cos α⋅ sin β
And of course, the second component is its antiprojection, which we can do by projecting in a perpendicular axis, v. We can construct this vector by reversing the coordinates of u and negating one of them:
c = <x,v> = cos α ⋅ cos β - sinα⋅ sin β
Some notes
So, now we have a way to generate circles, waves and many other undulating shapes and functions without using sin and cosine function, just by doing a couple of multiplications and additions instead per loop iteration. In theory we should be able to perform this tiny rotations per iteration for as many iterations as we wised, since

what means that R is neither a contracting nor expanding transformation indeed (it's a rotation after all!). Or in other words, we expect x to move in a perfect circle without every spiraling in or out. However due to numerical precision issues, x will eventually move in a spiral and fall into the origin. I never had this issue in my applications, but I'm guessing that for very big values of num, ie, little rotation angles, one can get some problems.
An example
In Kindercrasher, a realtime 4 kilobytes demo from 2008, a group of spheres do pulsate to the music. For that I computed the Fourier Transform of the sound in windows of 4096 samples (every frame though, so windows overlapped). Fast algorithms exist to do this in realtime, like the FFT. However, given that my code had to fit in no more than a few hundred bytes, I decided to do it in a different way. Instead of implementing the FFT I implemented the Discrete Fourier Transform directly from its very basic definition. You can check it on the Wikipedia.
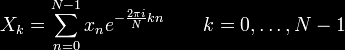
My function takes a stereo 16 bit sound buffer, x, and returns the first 128 frequencies in the sound spectrum of the sound in y. Note how the inner loop, that one iterating 4096 times, has no sin or cos calls, as the naive implementation would.
#include <math.h>
void iqDFT12( float *y, const short *x )
{
for( int i=0; i<128; i++ )
{
const float wi = (float)i*(2.0f*3.1415927f/4096.0f);
const float sii = sinf( wi );
const float coi = cosf( wi );
float co = 1.0f;
float si = 0.0f;
float acco = 0.0f;
float acsi = 0.0f;
for( int j=0; j<4096; j++ )
{
const float f = (float)(x[2*j+0]+x[2*j+1]);
const float oco = co;
acco += co*f; co = co*coi - si*sii;
acsi += si*f; si = si*coi + oco*sii;
}
y[i] = sqrtf(acco*acco+acsi*acsi)*(1.0f/32767.0f);
}
}








