Intro
This article proposes a small improvement to the box filtering of checker pattern, which introduced an analytic way to filter procedural checker patterns. By introducing a triangle shaped kernel, temporal stability can be improved for animated scenes over the original box filter version, at almost the same cost.

Aliased checkerboard

Analytic box filter

Analytic triangle filter
The Improvement
The problem with box filtering is that as the camera moves and a new feature starts overlapping a pixel's footprint, its contribution starts to affect the pixel's final color immediately. Depending on the scene, that can manifest as some flickering under camera animation (especially for slow moving cameras). One way to improve the situation is to replace the box filter by something that has a gradual contribution profile such that it zero at the edges of the kernel and gains relative weight at the center. Among the most common kernels used in CG film and games is the cubic filter. However, for this article we'll use triangular shaped kernel weights, which while not as good as the cubic, is still way way better than the box filter. In order to keep the image smooth we'll have to widen the kernel a little bit too.
In order to do so, we basically proceed exactly as in the box filter case, only that we have to change the form of the integral to account for the triangular kernel/window shape. For that, we have to replace the box filter formula:

with

Note that in reality the integrals run from uv-w/2 to uv+w/2, but re-centering the maths at 0 makes things easier to read. Remember also that f(x) is our square procedural signal.
The above integrals can be solved by using integration by parts, which produces some symmetries that cancel out to reduce to the following:
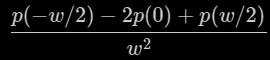
where p(x) is the integral of the triangular signal t(x), which was the integral of the square signal s(x):

The tricky part now is to compute p(x). Thankfully, the same way the triangular signal t(x) had an easy closed form, its integral (the double integral of the square signal) has it to. Since we know the area of each triangle is 1/2 and that the integral of a line is a quadratic curve, we can directly construct the p(x) as a connected parabolic arcs that rise one unit every two domain units. Below is a graph of the square signal s(x) in yellow, the triangular signal t(x) in red and its integral p(x) in blue:

This is the coded that returns the three signals s(x), t(x) and p(x), in a way that terms get reused nicely, which is good for performance (source code here):
// square signal and its first and second integrals
vec3 sqr_and_integrals( in float x )
{
x *= 0.5;
float h = fract(x)-0.5;
float s = -sign(h);
float t = 1.0 - 2.0*abs(h);
float p = x + h*t;
return vec3( s, t, p );
}
Now we have all that we need to perform the actual filtering:
vec2 p( in vec2 x )
{
vec2 h = fract(x/2.0)-0.5;
return x*0.5 + h*(1.0-2.0*abs(h));
}
// return a filtered checkers pattern
float checkersGradTriangle( in vec2 uv, in vec2 ddx, in vec2 ddy )
{
vec2 w = max(abs(ddx), abs(ddy)) + 0.01; // filter kernel
vec2 i = (p(uv+w)-2.0*p(uv)+p(uv-w))/(w*w); // analytical integral (triangle filter)
return 0.5 - 0.5*i.x*i.y; // xor pattern
}
It is worth noting that this code can be extended trivially to 3D by making all the vec2 functions a vec3.
The results are pretty good, although difficult to show in images or aniamted GIFs. I recommend visiting the realtime version and source code reference here: https://www.shadertoy.com/view/llffWs








