Planar ellipses (I add "planar" to make it clear it's not a 3D ellipsoid) are constructed by a 3D position c in space and two perpendicular orientation vectors u and v that define both the plane where the ellipse lays and the size of the axes. So you can store a 3D ellipse in 9 floats (8, if you are careful). In the case of the ellipse being degenerated to a disk, then a single orientation vector is needed (perpendicular to the plane containing the disk) and a radious (so, 6 floats). Planar ellipses can become very useful for computer graphics. For example, they appear when you cut a cylinder with a plane. They also appear when rendering point clouds with a splatting algorithm, or when raytracing point clouds. They can also help in realtime ambient occlusion and indirect lighting computations, where occluders can be approximated by a pointcloud.
Here I will show how to do two of the most basic operations on planar ellipses: bounding box calculation and ray intersection (sounds like this is what you need for a fast kd-tree based raytracer, uh?). Let's see the bounding box first:

The Bounding box of an ellipse computer analytically
As we know any point in the ellipse boundary is described by the following parametric equation:
p(ω) = c + u⋅cos(ω) + v⋅sin(ω)
With c, u and v defined as described above and as illustrated below:

The bounding box of the ellipse has to be tangent to this boundary. This tangential points will be the maximum and minimum x, y and z coordinates of the boundary equation. So, we need find the minima/maxima of the equation. We know that we can get them by finding where the derivative equal zero. So,
p'(ω) = -u⋅sin(ω) + v⋅cos(ω)
must equal zero for each of the three coordinates. Let's rename first λ=cos(ω)and solve for the x coordinate:
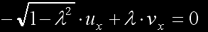
to get
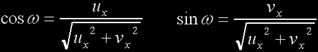
meaning that
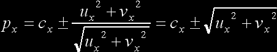
In summary, we can calculate our bounding box corners like this:

In (GLSL style) code this would become simply
You can find the source code and realtime demo using this code here: https://www.shadertoy.com/view/Xtjczw
Ready for building your acceleration kd-tree for point clouds?
Similarly to the ellipse border, the interior can be defined by
p(λ,γ) = c + u⋅λ + v⋅γ and λ2 + γ2 ≤ 1
where the equality holds for the border. Now, if we define the ray with the equation
p(t) = ro + t⋅rd
where ro is the ray origin and rd is the (not necessarily normalized) ray direction, then we must make both expressions equal in order to get the intersection point, thus we must solve the equation ro + t⋅rd = c + u⋅λ + v⋅γ that actually is a system of three equations (one for each of the x, y and z coordinates) with three unknowns. Re-arranging these three equations we get the following system:
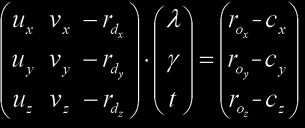
We can solve this by Cramer's law:
Note that de will be zero when the ray is parallel to the plane containing the ellipse, so that needs special care. Of course, t corresponds to the ray-plane intersection distance. Finally, to test that the intersection point is in the ellipse, check for
λ2 + γ2 ≤ 1
In code, this would mean
You can find the source code in the same location as the bbox code: https://www.shadertoy.com/view/Xtjczw
I hope all this is helpful for somebody :)
Here I will show how to do two of the most basic operations on planar ellipses: bounding box calculation and ray intersection (sounds like this is what you need for a fast kd-tree based raytracer, uh?). Let's see the bounding box first:

The Bounding box of an ellipse computer analytically
Bounding Box
As we know any point in the ellipse boundary is described by the following parametric equation:
p(ω) = c + u⋅cos(ω) + v⋅sin(ω)
With c, u and v defined as described above and as illustrated below:

The bounding box of the ellipse has to be tangent to this boundary. This tangential points will be the maximum and minimum x, y and z coordinates of the boundary equation. So, we need find the minima/maxima of the equation. We know that we can get them by finding where the derivative equal zero. So,
p'(ω) = -u⋅sin(ω) + v⋅cos(ω)
must equal zero for each of the three coordinates. Let's rename first λ=cos(ω)and solve for the x coordinate:
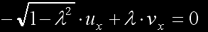
to get
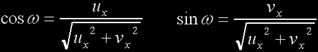
meaning that
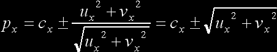
In summary, we can calculate our bounding box corners like this:

In (GLSL style) code this would become simply
// disk :: c:center, u: 1st axis, v: 2nd axis
bound3 EllipseAABB( in vec3 c, in vec3 u, in vec3 v )
{
vec3 e = sqrt( u*u + v*v );
return bound3( c-e, c+e );
}
You can find the source code and realtime demo using this code here: https://www.shadertoy.com/view/Xtjczw
Ready for building your acceleration kd-tree for point clouds?
Ray-ellipse intersection
Similarly to the ellipse border, the interior can be defined by
p(λ,γ) = c + u⋅λ + v⋅γ and λ2 + γ2 ≤ 1
where the equality holds for the border. Now, if we define the ray with the equation
p(t) = ro + t⋅rd
where ro is the ray origin and rd is the (not necessarily normalized) ray direction, then we must make both expressions equal in order to get the intersection point, thus we must solve the equation ro + t⋅rd = c + u⋅λ + v⋅γ that actually is a system of three equations (one for each of the x, y and z coordinates) with three unknowns. Re-arranging these three equations we get the following system:
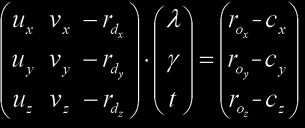
We can solve this by Cramer's law:
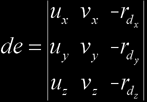 |
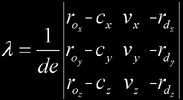 |
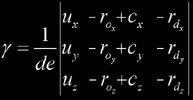 |
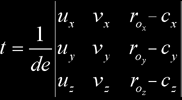 |
Note that de will be zero when the ray is parallel to the plane containing the ellipse, so that needs special care. Of course, t corresponds to the ray-plane intersection distance. Finally, to test that the intersection point is in the ellipse, check for
λ2 + γ2 ≤ 1
In code, this would mean
float iEllipse( in vec3 ro, in vec3 rd, // ray: origin, direction
in vec3 c, in vec3 u, in vec3 v ) // disk: center, 1st axis, 2nd axis
{
vec3 q = ro - c;
vec3 r = vec3(
dot( cross(u,v), q ),
dot( cross(q,u), rd ),
dot( cross(v,q), rd ) ) /
dot( cross(v,u), rd );
return (dot(r.yz,r.yz)<1.0) ? r.x : -1.0;
}
You can find the source code in the same location as the bbox code: https://www.shadertoy.com/view/Xtjczw
I hope all this is helpful for somebody :)








