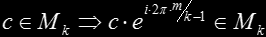Intro
When looking to pictures of the generalize Mandelbrot fc,k = zk + c one is tempted to make at least two observations. First, that the set seems to be always symmetric around the real axis. Second, the sets are symmetric under 2π⋅ m/(k-1) angle rotation. We will quickly show that both are indeed true.
Sets for k=2, 5 and 8, drawn with a distance estimation algorithm
Some pre math
We are going to concentrate on the Mandelbrot sets for monic one dimensional polynomials of the form fc,k = zk + c. Note that the critical point f 'c,k(z)=0 is the same
for all of them (zero), and that infinity is an super-attractive fixed point. The Mandelbrot set is defined as for the standard case k=2.
The set of point created by the iteration of zn+1 = fc,k(zn) with z0 = 0 is called the orbit of z0. Each point in the orbit is thus
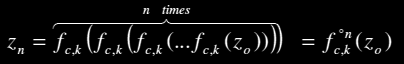
and when applied to z0 = 0 it expands the next polynomials in c:
So,
Tk0(c) = 0, Tk1(c) = c, Tk2(c) = ck + c
and so on. Then, a point c belongs to Mk if Tkn(c) stays bounded as n → ∞
The set of point created by the iteration of zn+1 = fc,k(zn) with z0 = 0 is called the orbit of z0. Each point in the orbit is thus
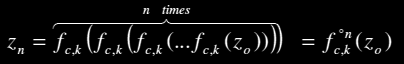
and when applied to z0 = 0 it expands the next polynomials in c:
So,
Tk0(c) = 0, Tk1(c) = c, Tk2(c) = ck + c
and so on. Then, a point c belongs to Mk if Tkn(c) stays bounded as n → ∞
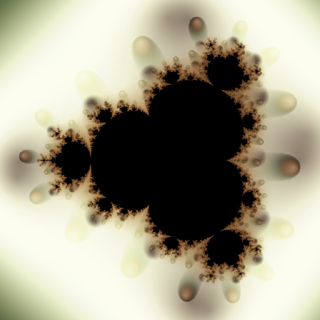
The Mandelbrot set for k=4
Vertical Symmetry
Vertical symmetry translates to saying that if a given point c belongs to the Mk set, then it's conjugate does also:
. The result comes from the fact that the iteration of
fc,k develops a polynomial in c with only real coefficients. But, let's show it anyway by induction.Let's assume that for one of the iterations we have
meaning that if c belongs to Mk then c* will also do, since the modulus of a complex number and its conjugate is the same. So, this Tkn(c) is symmetrical. Let's examine now what happens to the next iteration both for c
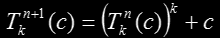
and for c*
From the property that for any complex number w and integer a we have
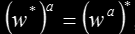, we conclude
and thus the next iterate is symmetrical too. In other words
Tkn(c) is symmetrical
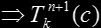is symmetricalWe just need to check that Tk1(c) = c is symmetric to arrive to the conclusion that all the iterates Tk are symmetrical.
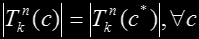
Therefore the complete Mk set is symmetrical around the real axis:
Rotational Symmetry
For the rotational symmetry we proceed in a similar way. Let's call a n-symmetry to a rotational symmetry of 2π⋅ m/n radians, for any integers m and n. Now, we first assume that one iterate Tkn(c) is (k-1)-symmetric as the pictures suggest. That translates to
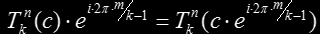
and now we try to demonstrate that next iterate will also be symmetrical. For that we analyze the iteration:
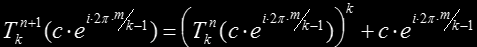
By the assumption we made,
So, again,
Because we can easily check that for n=1 the assumption holds, and because |w⋅ eiα| = |w| we can say that
Or put it in other way,
