Intro
It's very usual to people to know that for the classic Mandelbrot set the period two hyperbolic component H22 is a disc of radius 1/4 centered at -1. This result can be obtained easily by hand. However, is it possible to find a general method to obtain descriptions of Mandelbrot sets with k other than 2?
Period-2 bulbs in the Mandelbrot sets for k=2 and 3
k = 2
We start by imposing that the after some iteration n, the map
must have a fixed point:z = (z2+c)2+c → z4 + 2c⋅z2-z+(c2+c) = 0
We know that points in the main hyperbolic component have an converging orbit, and since convergence can be considered as being periodic of period 2 as well, we have to extract the hidden solution that represents H21 from the previous polynomial. For period 1 we have
z = fc(z) → z2 - z + c = 0
So we do the division
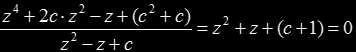
The derivative must be analyzed as for ensuring the convergence:
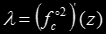
and by the chain rule
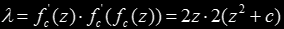
For easier later manipulation, we make the change of variable γ = λ/4. Then, the boundary of H22 in the c plane,
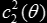, will be given by the fixed point theorem's constrain |λ| = eiθ (and the interior when the modulus
is less than one and hence the iteration converges) so we should be able to isolate z from one of the equations, and substitute in the other one to get c as a function
of λ. There is a technique called "resultant elimination" that is quite simple to use:
We now undo the change of variable c = -1 + λ/4 and impose the boundary condition to get
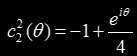
which is the circle centered in the c=-1 and radious 1/4 shown in the left in the first image in this article. To see how to apply this formula to speed up the rendering of the Mandebrot set, visit this entry https://www.shadertoy.com/view/4sdXWX in Shadertoy.
k = 3
Let's follow exactly the same steps for the case k=3. The second iterate must be equal to the iterated value, so
Again, this should be divisible by the period 1 polynomial
like this:
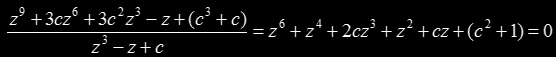
For the derivative,
Now we do the change of variable γ2 = λ/9 and get
Applying the resultant elimination method to this results in a 11x11 determinant:
and after undoing the change of variable,
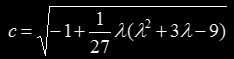
or in other words,
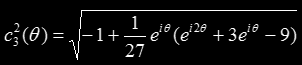
Because of the square root we can conclude that there will be two hyperbolic components of period two, both symmetrical around the origin, as seen in the right in the image opening this article.
Comparing the formulas for the
one is tempted to believe that in general there will be k-1 hyperbolic components of period two, with a formula of the type