When doing looking for size optimization it's always a good idea to apply some basic algebra and expand expressions and try to factorize them again in a different way to see if the same result can be expressed in less code (usually at the expense of speed of accuracy). Calculating polygon normals and areas is one of those cases(say, for a mesh).

In fact, this is true for n-sided polygons. You can easily demonstrate this yourself by drawing a pentagon, then an hexagon, and generalizing the idea. The result is that for n vertices vi with i={0, 1, 2, ...n-1} forming a polygon,
normal(v0, v1, ..., vn-1) = ∑vi ₓ vi+1
where of course the i+1 wraps to 0 when it otherwise becomes n.
This is extremely useful trick for 4 kilobyte demo coding, when you want to avoid doing some vertex subtractions in order to compute your face normals (and vertex normals too, as explained in the article about clever 3D mesh normalization. The problem this technique might have arises in the cases where the polygons or mesh are big and some of its vertices are far from the origin. In that case the cross products might be dealing with very parallel vectors and the precision of the result might be compromised. THe regular method of computing normals doesn't suffer from this as vertices get subtracted form each other. However, for most use cases, the method presented here works just fine. Promise.
The triangle
Let's define a triangle ABC in 2 or 3D, defined by its three vertices A, B and C. We now want to compute its area or normal vector - remember that the area is half the length of its normal. The classic approach to computing it is to first compute the edge vectors B-A and C-A and then cross them:
normal(A,B,C) = (B-A) x (C-A)
and therefore
area(A,B,C) = |normal(A,B,C)|/2
where |v| means the length of v. Now, let's expand the cross products, by distribution:
(B-A) x (C-A) = BxC - BxA - AxC + AxA
Since the cross product is anticommutative, BxA = -AxB, and since AxA = 0 (for it defines a zero area triangle), we get that
normal(A,B,C) = AxB + BxC + CxA
which is the sum of one cross product per side of the triangle. We can evaluate it by traversing all the vertices in order and cyclically, and doing the cross product with the following vertex. Not only this is interesting as an alternative way to compute triangle normals without edge vectors, but it also hits at some sort of generalization to polygons with more sides.
normal(A,B,C) = (B-A) x (C-A)
and therefore
area(A,B,C) = |normal(A,B,C)|/2
where |v| means the length of v. Now, let's expand the cross products, by distribution:
(B-A) x (C-A) = BxC - BxA - AxC + AxA
Since the cross product is anticommutative, BxA = -AxB, and since AxA = 0 (for it defines a zero area triangle), we get that
normal(A,B,C) = AxB + BxC + CxA
which is the sum of one cross product per side of the triangle. We can evaluate it by traversing all the vertices in order and cyclically, and doing the cross product with the following vertex. Not only this is interesting as an alternative way to compute triangle normals without edge vectors, but it also hits at some sort of generalization to polygons with more sides.

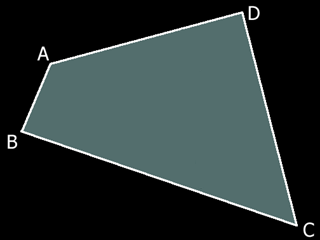
The quad
Let's define a quad ABCD by its four vertices A, B, C and D. We will compute both its surface area and normal as the sum of the aras and normals of two of the triangles it is composed of. This will work just fine for the surface areas, and for the normals too as long as the two triangles are coplanar and do define a real quad. In case they don't, the addition of the two normals will be nothing but the average normal of the quad. In any case, we have that:
normal(A,B,C,D) = normal(A,B,D) + normal(B,C,D) = AxB + BxD + DxA + BxC + CxD + DxB.
Again, due to the anticommutativity of the cross product (BxD = -DxB) we get that
normal(A,B,C,D) = AxB + BxC + CxD + DxA
which is again a cyclic alphabetically sorted sum of one cross product per side of the polygon. Nice!
Of course, again, area(A,B,C,D) = |normal(A,B,C,D)|/2
Interestingly, the normal/area of the quad can be also expressed as the cross of the diagonals: (A-C)x(B-D). Indeed, if you apply distribution and anticommutativity to this cross product, you will see it reduces to the same cyclic summatory of cross products.
normal(A,B,C,D) = normal(A,B,D) + normal(B,C,D) = AxB + BxD + DxA + BxC + CxD + DxB.
Again, due to the anticommutativity of the cross product (BxD = -DxB) we get that
normal(A,B,C,D) = AxB + BxC + CxD + DxA
which is again a cyclic alphabetically sorted sum of one cross product per side of the polygon. Nice!
Of course, again, area(A,B,C,D) = |normal(A,B,C,D)|/2
Interestingly, the normal/area of the quad can be also expressed as the cross of the diagonals: (A-C)x(B-D). Indeed, if you apply distribution and anticommutativity to this cross product, you will see it reduces to the same cyclic summatory of cross products.

And beyond
In fact, this is true for n-sided polygons. You can easily demonstrate this yourself by drawing a pentagon, then an hexagon, and generalizing the idea. The result is that for n vertices vi with i={0, 1, 2, ...n-1} forming a polygon,
normal(v0, v1, ..., vn-1) = ∑vi ₓ vi+1
where of course the i+1 wraps to 0 when it otherwise becomes n.
Conclusions
This is extremely useful trick for 4 kilobyte demo coding, when you want to avoid doing some vertex subtractions in order to compute your face normals (and vertex normals too, as explained in the article about clever 3D mesh normalization. The problem this technique might have arises in the cases where the polygons or mesh are big and some of its vertices are far from the origin. In that case the cross products might be dealing with very parallel vectors and the precision of the result might be compromised. THe regular method of computing normals doesn't suffer from this as vertices get subtracted form each other. However, for most use cases, the method presented here works just fine. Promise.








